다중 목표 최적화 문제 - 차원의 저주에 걸린 고전 기법들 (1)

다중목표 최적화 문제(multiobjective optimization problem)은 목표가 2개 이상인 최적화 문제이다. 비용을 최소화하거나 성능을 최대화시키는 등의 일반적인 단일 목표 최적화 문제들은 random search나 gradient descent와 같은 기법으로 탐색이 가능한 반면, "비용은 최소화하고 성능을 최대로 만들고 싶다"는 여러 개의 목표를 동시에 달성하고 싶은 상황에 적용하기 좋은 알고리즘이다.

 

예를 들어, 대부분의 공학 문제는 비용을 최소화히고, 성능을 최대화하는 것을 목표로 하는 다중목표 최적화 문제에 해당한다. 물론,

효율 = 성능 / 비용

과 같은 새로운 단일목표를 도입하여 최적화하기도 한다. 하지만, 첫째로 이런 단일목표가 과연 좋은 단일목표인지도 알 수 없고, 둘째로 이 경우는 목표가 두 개일 뿐이지만 목표가 세 개, 네 개, ...로 다양해질수록 좋은 단일목표를 제시하기도 어려워진다.

 

다중목표 최적화 문제 (multi-objective optimisation problem)는 다음과 같이 정의된다.

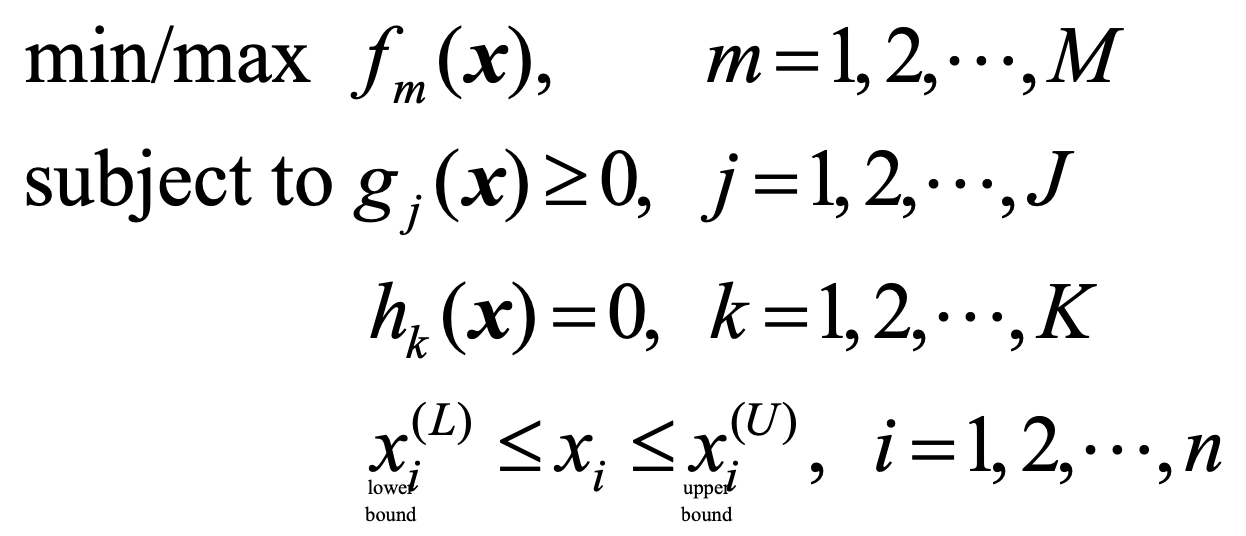
즉, 첫번째 줄의 m개의 목표 함수 (fitness function)를 최적화하고 싶고, 이 때, 고려하는 해 공간 (solution space)는 둘째 줄 이후부터의 조건들을 따라야 한다.

 

이 글에서는 다중 목표 최적화를 할 수 있는 알고리즘들을 소개하는 것을 목표로 한다. 우선 해들이 어떤 관계를 가지고 어떤 공간에 펼쳐져 있는지를 살펴보고, 그 다음으로 다중 목표 최적화 문제를 푸는 기법들인 가중 합, 입실론-조건, 그리고 탐색 기반의 알고리즘들을 살펴볼 예정이다.

 

해의 우열관계 (dominance relation)

다중목표탐색 알고리즘은 목표가 여러 개이기 때문에, 최적해(optimal solution)의 정의가 까다롭다. 예를 들어, 비용을 최소화, 성능을 최대화하고 싶을 때 다음과 같은 해들이 주어졌다 하자:

• \(x_1\): 비용 = 5, 성능 = 10.
• \(x_2\): 비용 =3, 성능 = 7.
• \(x_3\): 비용 = 9, 성능 = 2.

어떤 해가 더 좋은 지를 생각해볼 때 두 가지 점을 관찰할 수 있다. 첫 번째로, \(x_1\)과 \(x_2\)의 우열관계가 분명하지 않다. \(x_1 < x_2\)라고 쓰기에는 \(x_2)의 성능보다 \(x_1\)의 성능이 더 좋고, \(x_1 > x_2\)라고 하기에는 비용은 \(x_2\)가 더 적게 든다. 두 번째로, 해 \(x_3\)은 \(x_1\)과 \(x_2\)보다 좋지 않은 해이다. 비용은 가장 비싸고, 성능은 가장 낮게 나오기 때문에 \(x_3 < x_1\)이고 \(x_3 < x_2\)인게 확실하다.

 

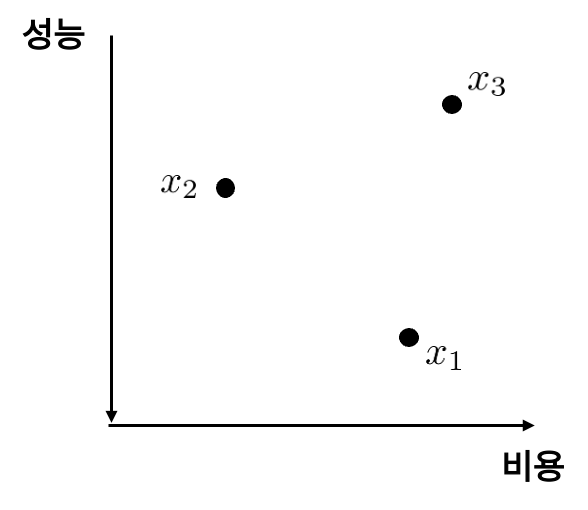
x1과 x2는 비교 불가능하고, x3은 열등한 이유를 좌표평면에 그려봐도 직관적으로 알 수 있다. 목표는 평면에서 좌하단으로 갈수록 달성되는데, x3은 어떤 해와 비교해도 우측 상단에 위치해있기 때문에 별 가치가 없다. 엄밀하게는 다음과 같이 적을 수 있다.

 

정의. (우열 관계, dominance relation) 최적화 목표가 \(f_1, f_2, \cdots, f_n\)을 최소화하는 것일 때 해 \(x_A\)가 해 \(x_B\)보다 우등하다는 것은 $f_i(x_A) < f_i(x_B)$가 모든 $i$에 대해서 성립한다는 것을 의미한다.

 

부분순서(partial order)를 알고 있다면, 우열 관계는 대표적인 부분순서 관계임을 쉽게 이해할 수 있다.

파레토 최적 전면 (Pareto-optimal front)

우열 관계 맥락에서 살펴보았을 때, 결국 다중목표 최적화 문제에서 찾고자 하는 해는 그보다 우등한 해가 없는 해이고, 이들을 파레토-최적 해(Pareto-optimal solutions)라고 한다. 

 

실현 가능한 모든 해들을 좌표 평면에 모아놓으면 다음과 같이 어떤 면(surface)을 형성한다.

 

최적화 목표가 \(f_1, f_2\)을 최소화 시키는 것이라고 하면, 이 중 파레토-최적 해는 초록색으로 표시한 해들이다.

 

즉, 실현 가능한 모든 해들 중 파레토-최적 해들을 모아 놓으면, 어떤 공간의 경계를 찾는 형태가 된다. 이 경계를 파레토 최적 전면(Pareto-optimal front)라고 하고, 다중목표 최적화 문제의 목표는 파레토 최적 해들로 이루어진 파레토 최적 전면을 실현 가능한 해 공간에서 찾는 것이 된다.

 

다중목표 최적화 문제의 목표는 파레토 최적해들로 이루어진 파레토-최적 전면에 최대한 가까운 해들을 실현 가능한 해 공간에서 찾는 것이다.

 

그러면 지금부터 다중목표 최적화 문제 해결 기법들을 하나씩 알아보자.

1. 가중 합 (weighted sum)

가중 합은 목표 함수를 하나로 만들 때 선형적인 관계만을 사용한다. 즉, 목표가 \(f_1, f_2, \cdots, f_n\)을 최소화 시키는 것일 때, 새로운 단일 목표 함수

\[F(x) = \sum _{i=1} ^n w_i f_i (x)\]

를 최소화하도록 최적화 목표를 설정하는 방법이다. 이 때 가중치 \(w_i\)들은 임의로 설정하는 양의 값들이다. 여러 개의 목표를 하나로 합쳐 만들어진 단일목표를 최적화 기법으로 하는 접근이다.

 

• 장점
  • 단순하다.
• 단점
  • 가중치 설정값 \(w_i\)을 주어진 해 공간에 적합하게 설정하기 까다롭다.
  • 파레토-최적 해의 어떤 부분은 볼록하지 않은 해 공간에서는 발견되지 않는다.
  • 다양한 파레토-최적 해를 찾기 위해서는 여러 가중치 설정 값으로 단일목표 최적화를 반복해야 한다.

특히 두 번째 단점은, 다음 그림에서 볼 수 있다.

가중치를 설정하고 가중 합을 최적화하는 것은, 해 공간과 겹치는 부분이 있는 상태에서 최대한 좌측 하단에 있는 일정한 기울기의 직선을 찾는 것과 같다. 가중치와 가중 합의 결과가 고정되어 있다면, \(f_1\)과 \(f_2\)는 선형 관계를 가지기 때문이다. 그리고 좌측 하단으로 움직일수록 가중 합의 결과가 작아지는, 목표 함수가 최적화되는 것과 같다. 즉, 가중 합 기법은 해 공간의 좌측 하단에서 접하는 고정된 기울기의 직선과 접하는 점들을 파레토-최적 해로 인식하는 기법이다.

하지만, 빨간 색으로 표시한 해 공간에서 오목한 부분의 파레토-최적 해들은 가중 합 기법으로는 절대 찾을 수가 없다. 왜냐하면 이들에 접하는 직선보다 좌측 하단에 있는 직선들이 존재하고, 이는 즉 가중 합의 단일목표가 더 최적화되는 경우가 언제나 존재하기 때문이다.

 

세 번째 단점은, 다양한 파레토 최적해를 찾으려면 다양한 가중치 설정값으로 단일목표 최적화를 반복해야 한다는 부분이다. 결국 다중목표 문제를 단일목표 문제로 단순화시키면 고정된 가중치 설정값으로 찾을 수 있는 파레토 최적해가 제한되기 때문이다. 이것도 일정의 '차원의 저주'로, 고차원의 목표 문제를 저차원에서 풀 수 없다.

2. 입실론 조건 (epsilon constraint)

다중 목표 중 목표 한 개만 최적화하고, 나머지 목표들은 조건 제한만 두고 최적화하지 않는 기법이다 (Haimes et al, 1971).

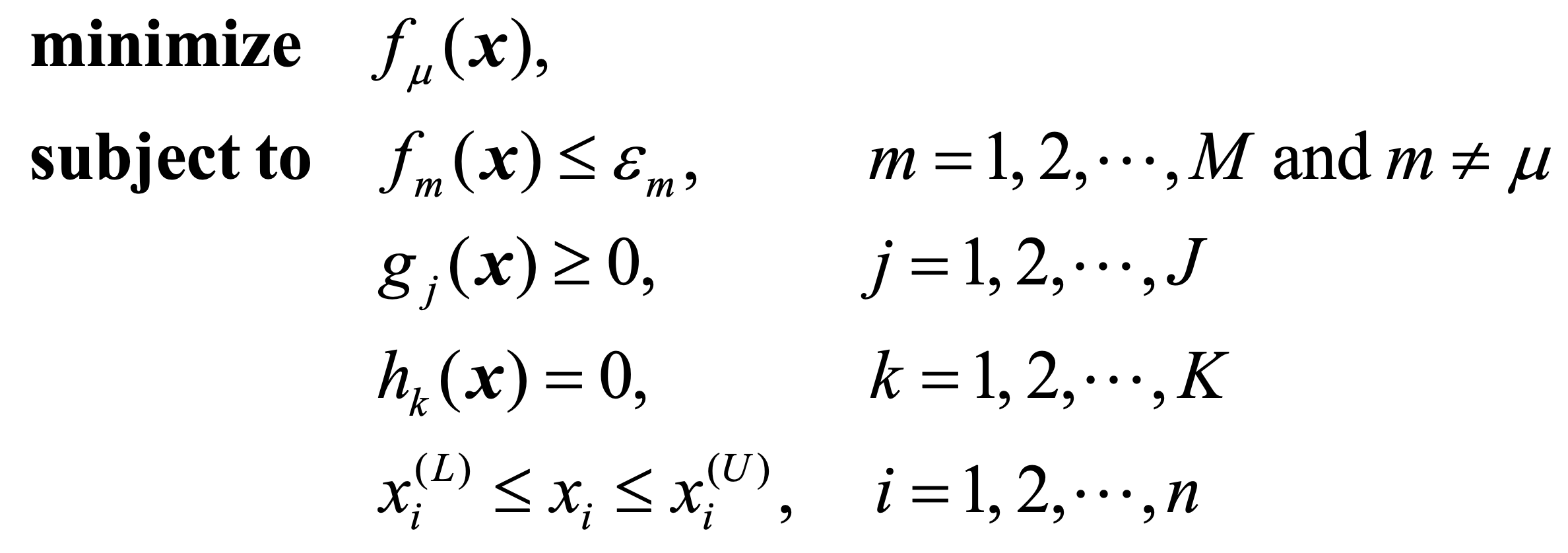
이 단일목표 최적화 문제를 풀기만 하면, 파레토-최적 해를 찾을 수 있다.

예를 들어, 목표가 \(f_1, f_2\) 두 개를 최소화하는 상황에서, \(f_1(x) < \epsilon\)으로 조건을 고정하고 \(f_2\)만 최소화하는 방향의 최석화를 하면 위와 같은 그림이 된다. 가장 진하게 표시된 점이 \(f_2\)를 가장 최적화 한 결과이고, 이는 파레토-최적해에 가장 가깝다.

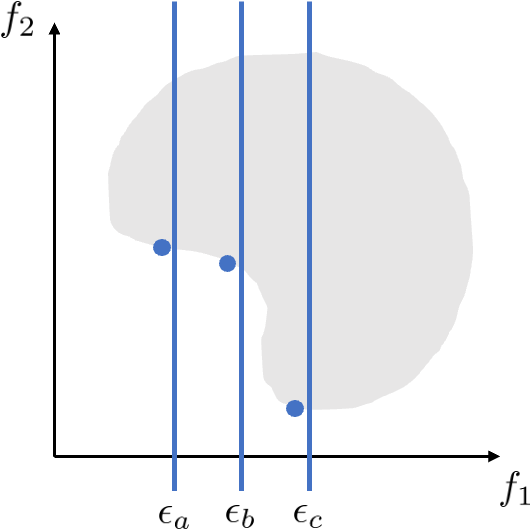
입실론 조건을 조정해가면서 최적화를 여러 번 적용하면 위 그림과 같이 파레토-최적에 가까운 해들을 찾을 수 있다.

 

• 장점
  • 볼록하지 않은 해 공간에서도 입실론 조건을 정확하게 설정한다면 모든 파레토 해들을 찾아낼 수 있다.
• 단점
  • 좋은 입실론 조건 벡터를 설정하는하는 것이 까다롭다.
  • 다양한 파레토-최적 해를 찾기 위해서는 여러 가중치 설정 값으로 단일목표 최적화를 반복해야 한다.

첫 번째 단점은 입실론 값을 해 공간 밖에 있는 범위로 잡아버리면 아예 해를 찾는 것이 불가능하기 때문에, 최적화를 시작하지도 못한다는 의미이다. 특히 목표가 많아질수록 공간도 복잡해질 것이고, 좋은 입실론 조건을 설정하는 게 까다로울 수도 있다.

 

두 번째 단점은 가중 합 기법과 공유하는 단점으로, 역시 특정 입실론 조건 벡터에서는 특정 최적해만을 찾을 수 있기 떄문이다. 즉, 차원의 저주가 여기에도 해당한다. 단일 목표로 문제를 바꿔버리면 그 대가로 다양한 입실론 조건 설정에서 단일 목표 탐색을 수행해야 한다.

 

다음 글에서는 이어서 다중 목표 탐색 알고리즘 (Multi-objective search algorithm, MOSA)를 소개하겠다.

 

출처

[1] https://engineering.purdue.edu/~sudhoff/ee630/Lecture09.pdf