[LeetCode] 135. Candy - 풀이와 증명
Candy
총평: O(n)짜리 풀이가 생각하기 힘들다. 특정 유형을 적용해서 푸는 문제라기보다는 직접 관찰하고 알고리즘을 설계하는 게 중요한 편에 속한다.
난이도: Hard
문제 설명
There are n children standing in a line. Each child is assigned a rating value given in the integer array ratings.
You are giving candies to these children subjected to the following requirements:
- Each child must have at least one candy.
- Children with a higher rating get more candies than their neighbors.
Return the minimum number of candies you need to have to distribute the candies to the children.
Example 1:
Input: ratings = [1,0,2]
Output: 5
Explanation: You can allocate to the first, second and third child with 2, 1, 2 candies respectively.
Example 2:
Input: ratings = [1,2,2]
Output: 4
Explanation: You can allocate to the first, second and third child with 1, 2, 1 candies respectively.
The third child gets 1 candy because it satisfies the above two conditions.
풀이
우선 rating을 \(r_1, r_2, \cdots, r_n\)으로 봤을 때, 각 아이에게 준 사탕의 수를 \(c_1, c_2, \cdots, c_n\)이라고 두면 \(c_i\)는 다음 성질을 만족해야 한다.
- \(r_i > r_{i+1}\)이면 \(c_i > c_{i+1}\)을 만족해야 한다.
- \(r_i > r_{i-1}\) 이면 \(c_i > c_{i-1}\)을 만족해야 한다.
- \(c_i \ge 1\)이다.
이렇게 할 때 \(\sum c_i\)가 최소가 되도록 사탕을 배분하는 방법을 찾아야 한다.
다음은 글쓴이의 삽질 기록이니 궁금한 사람만 보시라..
하나 확실한 것은, 최소의 rating을 가지는 학생은 1을 주면 된다는 점이다.
왜냐하면 최소의 rating을 가지는 학생의 이웃은 그 학생보다 큰 사탕을 주기만 하면 되니까, 하한이 존재하지 않고 최소 기준인 1만 맞추면 되기 때문이다.
전체 구간에서 최소 rating의 학생에게 줄 사탕의 양을 정하면, 그걸로 전체 구간은 두 부분으로 쪼개지게 된다.
그래서 각 구간에 대해 같은 과정을 적용하는데, 이 때 만약 여기서 찾은 최소 rating의 학생이 구간의 양 끝에 있을 경우에 그 구간 밖에 준 사탕의 양도 고려하여 그보다 큰 최소한의 양을 주면 된다.
이런 식으로 divide-and-conquer 방식으로 문제를 해결할 수 있다.
그래서 각 구간별로 최소 rating을 가지는 학생의 인덱스를 기록하는 세그먼트 트리를 초기화하는데 O(nlogn)이 들고,
분할정복 함수는 n번 호출되고 최소값 쿼리는 O(log n)이므로, 분할정복할 때 드는 시간도 결국 O(nlogn)이 된다.
func candy(ratings []int) int {
// bottom-up segment tree for minimum indices
l := 1
n := len(ratings)
m := n
for m > 0 {
m = m >> 1
l = l << 1
}
segtree := make([]int, 2*l)
for i:=0; i<2*l; i++ {
segtree[i] = -1
}
for i:=0; i<n; i++ {
j := l+i
for j > 0 {
if segtree[j] == -1 {
segtree[j] = i
} else {
i1 := segtree[j]
if ratings[i1] > ratings[i] {
segtree[j] = i
}
}
j = j >> 1
}
}
var find_min func(start int, end int) int
find_min = func(start int, end int) int {
if start == end {
return segtree[start]
}
res := -1
if start % 2 == 1 {
i := segtree[start]
if res == -1 || ratings[res] > ratings[i] {
res = i
}
start += 1
}
if end % 2 == 0 {
i := segtree[end]
if res == -1 || ratings[res] > ratings[i] {
res = i
}
end -= 1
}
start = start >> 1
end = end >> 1
if start <= end {
i := find_min(start, end)
if res == -1 || ratings[res] > ratings[i] {
res = i
}
}
return res
}
candy := make([]int, n)
for i:=0; i<n; i++ {
candy[i] = -1
}
var divide_and_conquer func(left int, right int)int
divide_and_conquer = func(left int, right int) int {
if left > right {
return 0
}
i := find_min(left+l, right+l)
min_candy := 1
if i > 0 {
if candy[i-1] != -1 && ratings[i] > ratings[i-1] {
min_candy = max(min_candy, candy[i-1]+1)
}
}
if i < n-1 {
if candy[i+1] != -1 && ratings[i] > ratings[i+1] {
min_candy = max(min_candy, candy[i+1]+1)
}
}
candy[i] = min_candy
return divide_and_conquer(left, i-1) + min_candy + divide_and_conquer(i+1, right)
}
return divide_and_conquer(0, n-1)
}
예를 들어 rating이 [1,3,6,8,9,5,3,6,8,5,4,2,2,3,7,7,9,8,6,6,6,4,2]이었다면
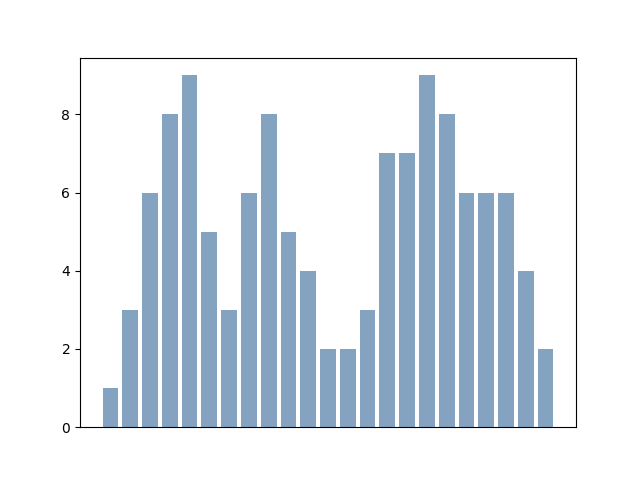
다음과 같이 분포되어있을 것이다. 그렇다면 \(c_i\)에 얼마의 사탕을 주어야 할까?
시작점인 \(c_0\)부터 생각해보자. \(c_0\)에는 1을 주어야 한다. 이유는? 귀류법을 통해 접근이 가능한데, 어떤 최적해가 \(c_0 \ne 1\)이라고 가정하자. 그러면 \(c_0 > 1\)인데 여기서 \(c_0\)를 1로 교체한 해 또한 위의 성질들을 모두 만족한다. 그래서 가정은 거짓이고, \(c_0 = 1\)이어야만 한다.
두 번째는 어떨까? \(c_1\)에는 2를 주어야 한다. \(c_1\)에 1을 주는 건 불가능한 이유가, \(c_1 > c_0\)을 만족해야 하기 때문이다. 하지만 \(c_1 > 2\)를 주는 것은 또 낭비인게, 그런 최적해가 존재한다고 가정하면 \(c_1=2\)로 대체해도 그 해는 위 조건들을 만족하기 때문이다.
이런 식으로 \(c_2=3\), \(c_3=4\)까지 주어진다.
첫 번째로 만난 봉우리에서 \(c_4=5\)일까? 결론부터 말하자면 '그렇다'이지만, 왜 그럴까?
이걸 확인하려면 다음 '골짜기'인 \(c_6\)에서 시작해야한다.
\(c_6=1\)이 되어야 한다. \(c_6 < c_5, c_7\)을 만족하기만 하면 되기 때문에, \(c_0\)와 같은 논리로 \(c_6\)은 1을 주는게 최적이다.
\(c_5=2\)가 되어야 한다. \(c_5 > c_6\)을 만족하면서 가장 작은 경우가 \(c_5=2\)이기 때문이다.
이제 \(c_5\)에서 생각해볼 차례다. 이전에 \(c_3=4\), \(c_5=2\)인게 확인되었고, \(c_4\)로는 \(c_3\)와 \(c_5\)보다 큰 값을 주면 된다.
이 조건을 만족하는 가장 작은 \(c_4\)는 4와 2보다 큰 최소 정수인 5이다.
여기서 다시 \(c_4=5\)가 되는 이유를 생각해보면, 왼쪽으로 갈 때 rating이 감소하는 입접한 원소들의 최대 길이는 \(r_4, r_3, r_2, r_1, r_0\)이고 오른쪽으로 갈 때 rating이 감소하는 인접한 원소들의 최대 길이는 \(r_4, r_5, r_6\)이고 각각 길이가 5와 3이고, 이 중 길이가 5가 되는 가장 최적의 수열은 \(5, 4, 3, 2, 1\)이기 때문에 \(c_4=5\)를 부여하게 된다.
이 성질은 \(c_4\)와 같은 봉우리 뿐만 아니라, 더 일반화해서 모든 학생에게도 적용 가능하다. 즉, 최적해의 i번째 학생에게 주는 사탕의 양 \(c_i\)는 \(c_i\)에서 출발했을 때 max(왼쪽으로 가는 인접한 감소하는 수열의 최대 길이, 오른쪽으로 가는 인접한 감소하는 수열의 최대 길이)가 된다. 주변부보다 작은 '골짜기'에 해당하는 곳은 1을 주고, 거기서부터 1칸씩 높이면서 귀납법을 적용하면 좀 더 formal한 증명이 된다.
따라서, 이 문제는 배열을 두 번 순회해서 왼쪽으로 가는 인접한 감소하는 수열의 최대 길이와 오른쪽으로 가는 인접한 감소하는 수열의 최대 길이를 기록한 후, 최종적으로 i번째 학생마다 왼쪽 수열, 오른쪽 수열의 길이 최대값만큼의 사탕을 주면 된다.
Go로 작성하면 다음과 같다:
func candy(ratings []int) int {
n := len(ratings)
left_dec_len := make([]int, n)
right_dec_len := make([]int, n)
for i:=0; i<n; i++{
if i == 0 || ratings[i] <= ratings[i-1] {
left_dec_len[i] = 1
} else {
left_dec_len[i] = left_dec_len[i-1] + 1
}
}
for i:=n-1; i>=0; i--{
if i == n-1 || ratings[i] <= ratings[i+1] {
right_dec_len[i] = 1
} else {
right_dec_len[i] = right_dec_len[i+1] + 1
}
}
x := 0
for i:=0; i<n; i++ {
x += max(right_dec_len[i], left_dec_len[i])
}
return x
}
이렇게 하면 O(n)의 시간복잡도와 공간복잡도를 가지는 알고리즘으로 문제가 해결된다.
