개미 군집 알고리즘: 개미의 먹이 탐색으로부터 영감을 받다

개미는 인간과 닮았다. 아니, 어쩌면 인간이 개미를 닮은 것인지도 모른다.

 

베르나르 베르베르의 《개미》는 단순한 곤충의 이야기를 넘어선다. 그 속에서 우리는 개미 군집의 조직력, 생존 전략, 그리고 협업의 아름다움을 발견한다. 수많은 개체가 하나의 목표를 위해 움직이는 모습은 단순히 생물학적인 호기심을 넘어 인간 사회에도 깊은 영감을 준다.

 

개미 군집 알고리즘은 바로 이러한 개미들의 행동에서 영감을 받아 탄생한 과학적 기법이다. 자연에서 관찰되는 개미의 길 찾기, 자원 배분, 문제 해결 방식이 오늘날 컴퓨터 과학과 최적화 문제를 해결하는 데 혁신적인 방법론으로 자리 잡았다. 이 글에서는 개미 군집 알고리즘(Ant Colony Optimization, ACO)의 매력을 탐구하며, 자연이 우리에게 준 또 하나의 선물에 대해 이야기하고자 한다.

 

개미는 혼자가 아닌 집단으로 움직일 때 비로소 놀라운 능력을 발휘한다. 개미들이 먹이를 찾고 최적의 경로를 만드는 데 핵심적인 역할을 하는 것은 바로 정찰 개미와 페로몬(pheromone)이다.

 

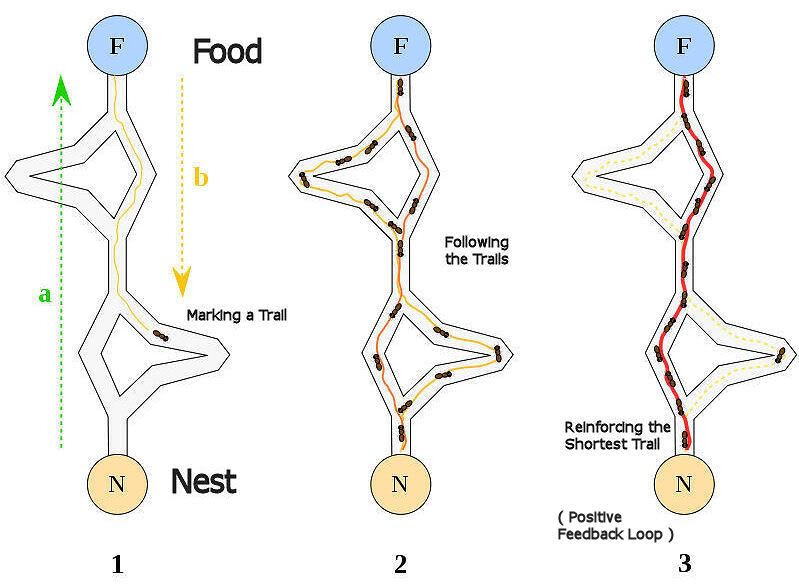
처음에 개미 집단은 주어진 환경에서 무작위로 움직이며 먹이를 탐색한다. 이 과정에서 일부 정찰 개미는 운 좋게 먹이를 발견하고, 그 위치로부터 둥지로 돌아가는 길에 페로몬을 남긴다. 이 페로몬은 일종의 화학적 신호로, 다른 개미들에게 "이 방향에 먹이가 있다"는 정보를 전달한다.

더 많은 개미가 같은 경로를 지나가면서 페로몬 농도가 점점 높아지면, 개미들은 자연스럽게 페로몬이 강한 경로를 선호하게 된다. 이렇게 경로를 반복적으로 사용하면서 페로몬이 강화된 길은 짧고 효율적인 최적 경로로 정제된다. 흥미로운 점은, 만약 다른 경로가 더 짧고 효과적이라면, 개미들은 이를 탐색하며 기존 경로를 대체할 수도 있다는 것이다. 페로몬은 시간이 지나면 휘발되기 때문에, 덜 사용되는 경로는 자연스럽게 사라지고, 전체 집단은 효율성을 유지할 수 있다.

이러한 행동은 개미 개체 하나로는 이루어질 수 없는 집단 지성의 대표적 사례다. 개미 군집 알고리즘은 바로 이 원리를 모방해 최적화 문제를 해결하는 데 활용된다.

 

개미 군집 최적화로 TSP 풀기

구체적으로, NP-완전 문제인 외판원 순회 문제(TSP)는 개미 군집 최적화로 다음과 같이 풀 수 있다. 편의상 모든 정점이 이어진 완전그래프를 가정한다. (2D 지도나 지구 구면과 같이 거리공간이 정해져 있다면 각 점의 좌표를 이용하여 점들 사이의 거리가 계산 가능하기 때문에 이런 가정을 해도 실용성을 많이 잃지는 않는다)

 

1. 초기화 (Initialisation)
개미 군집 알고리즘의 첫 단계는 그래프의 정점 위에 개미들을 무작위로 배치하는 것이다. 또한 그래프의 모든 간선에 소량의 페로몬을 균일하게 뿌려 시작한다.

 

2. 개미의 이동 결정
개미는 각 정점에서 어느 경로(엣지)를 따라 이동할지 확률적으로 결정한다. 이때, 두 가지 요인을 고려한다:

 

• 경로의 길이 (짧을수록 선호)
• 해당 경로 위에 존재하는 페로몬의 양 (많을수록 선호)
  이 두 요소를 기반으로 각 경로의 선택 확률을 계산한다.

정점 i에 있는 개미가 정점 j로 연결된 간선을 선택할 확률은 다음과 같다.

\[p_{ij} ^k = \frac{\tau _{ij} ^a \eta _{ij} ^b}{\sum _{h \in J^k} ^H \tau _{ih} ^a \eta _{ih} ^b }\]

• \(\eta_{ij} = \frac{1}{l_{ij})\)는 정점 i에서 j까지의 거리에 반비례하는, 짧은 간선의 우선순위를 높이는 값이다.
• \(\tau_{ij}\)는 i와 j 사이의 간선에 뿌려진 페로몬의 양이다.

a와 b는 거리와 페로몬 중 어떤 것을 더 집중적으로 볼 것인지를 결정하는 하이퍼파라미터로, a=0이면 간선의 길이에 의해서만 확률이 결정되고, b=0이면 페로몬의 양에 의해서만 확률이 결정된다. \(J^k\)는 개미가 아직 도달하지 않은 정점들을 나타낸다.

 

3. 투어 완료 후 페로몬 남기기
개미가 모든 노드를 지나며 한 차례 투어(여행)를 마치면, 자신이 지나온 경로를 따라 페로몬을 남긴다.

• 남기는 페로몬의 양은 경로의 길이에 반비례한다. (즉, 더 짧은 경로일수록 더 많은 페로몬을 남김.)

개미 k가 간선 ij에 뿌리는 페로몬의 양은 다음과 같다.

\[ \Delta \tau _{ij} ^k = \frac{Q}{L^k}\]

Q는 지금까지 발견된 가장 짧은 경로의 길이이고, \(L^k\)는 개미 k가 탐색한 경로의 전체 길이이다.

 

간선 ij에 새로 뿌려진 페로몬의 전체 양은 각 개미가 뿌린 페로몬 양의 합이다.

\[ \Delta T_{ij} = \sum _{k} ^M \Delta \tau _{ij} ^k\]

 

4. 페로몬의 증발 (Evaporation)
다음 라운드로 넘어가기 전에, 모든 경로에 남겨진 페로몬의 양은 일정 비율만큼 증발한다. 이는 이전 경로에 치우치는 것을 방지하고 새로운 경로 탐색을 유도하는 역할을 한다.

\[ \tau_{ij} ^{t+1} = (1- \rho) \tau_{ij} ^t + \Delta T_{ij} \]

\(\rho\)는 증발비율을 나타낸다.

 

5. 최적 경로로의 수렴 (Convergence)
시간이 지남에 따라, 더 짧고 효율적인 경로에 더 많은 개미가 몰리게 된다. 이는 해당 경로에 페로몬이 집중적으로 쌓이기 때문이다. 결과적으로, 모든 개미들은 최적 경로(가장 짧은 경로)에 수렴하게 된다.

 

지금까지 소개한 알고리즘은 하나의 예시로, 반드시 이대로 구현하라는 법은 없다. 하지만 개미가 간선을 선택할 때 페로몬이 영향을 주도록 만들고, 시간에 따라 페로몬이 증발한다는 점만 지키면 된다

 

다음은 berlin52라는 52개의 정점으로 이루어진 TSP문제에 ACO를 적용했을 때 경로가 점점 어떻게 개선되는지를 보여준다.

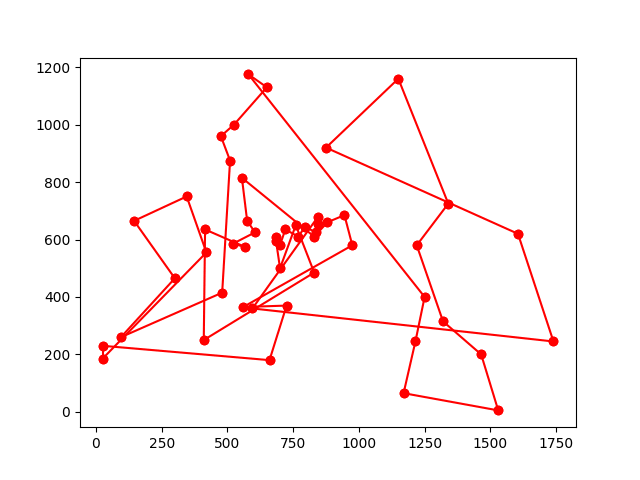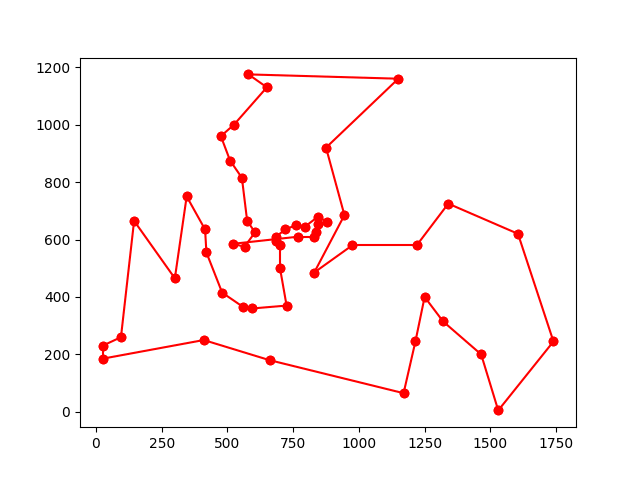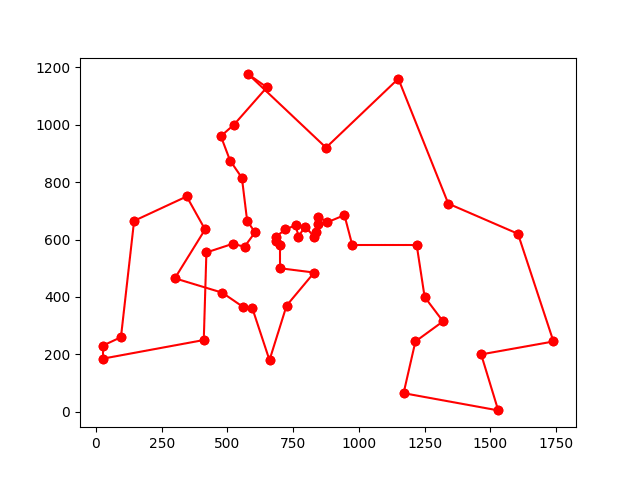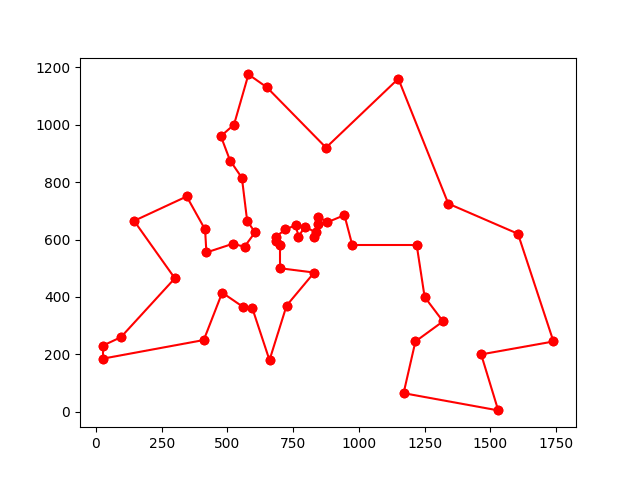
이 때 페로몬 그래프는 다음과 같다.

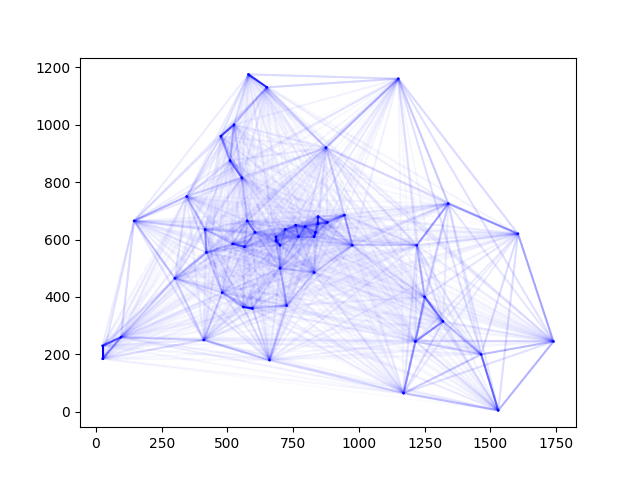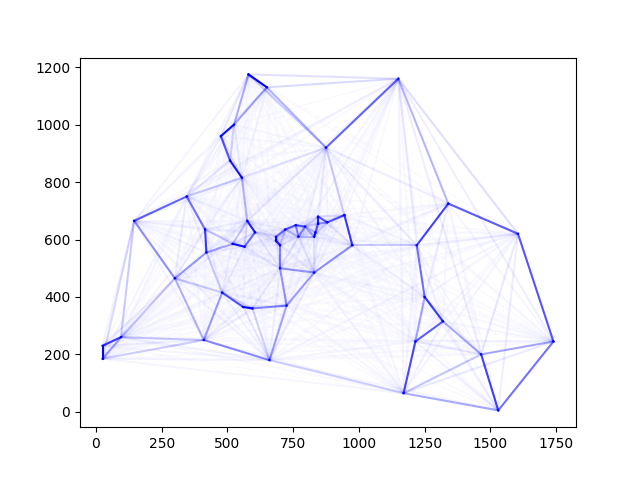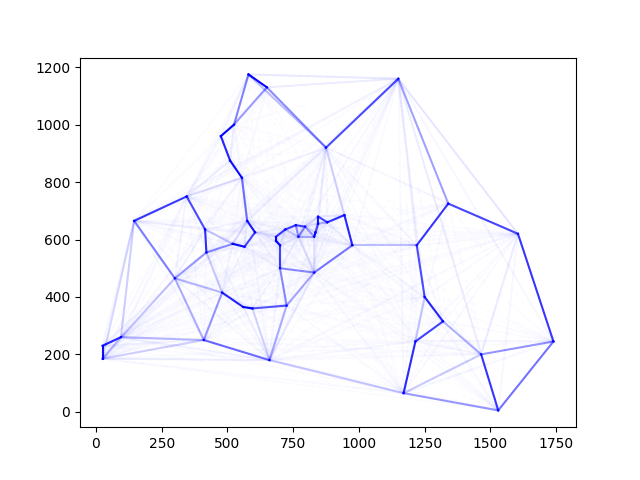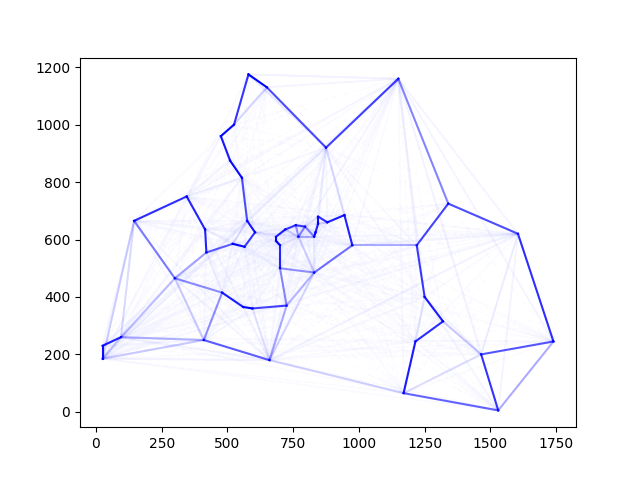
처음에 균일하게 뿌려놓은 페로몬이 시간이 지나면서 개미들이 자주 다닌 경로에 집중되는 것을 볼 수 있다.

 

장점

• 강력한 탐색 능력: 초기에는 무작위성을 통해 다양한 경로를 탐색하며, 점차적으로 최적 경로에 수렴한다.
• 적응성과 유연성: 탐색 도중에 그래프가 변하더라도 그에 맞춰서 최적해를 탐색할 수 있다.

단점

• 휴리스틱의 한계: 개미 군집 최적화로 찾은 해가 최적해임을 보장하지 않는다.
• 계산량 증가: 문제 크기(정점의 개수)가 증가하면 탐색해야 할 경로 수가 늘어나 계산량이 크게 증가한다.